合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
-
> 水和乙二醇-水混合體系中的離子液體-陽離子表面活性劑混合膠束自聚焦-電導法 表面張立法和光譜研究法—
> 克服表面張力使液態金屬可拉伸電子器件化的研究進展
> 表面張力的形成同處在液體表面薄層內的分子的特殊受力狀態密切相關。下列現象,與表面張力無關的是:
> 露珠為什么是球形的?這是液體的表面張力造成的!
> 酯功能化的雙子表面活性劑與血紅蛋白的結合——摘要、簡介
> 水面上單分子層膜通過磷脂光控開關實現可逆光學控制:結果和討論、結論
> 氟化石墨烯復合鍍層制備,如何減小電極和鍍液之間的界面張力
> ?白酒掛杯與表面張力有何關系
> 表面張力儀分子所受到的各個方向的力是相同的
> 座滴法測量玻璃熔體表面張力的影響因素研究
流體力學中的粘性
來源:LBM與流體科普 瀏覽 532 次 發布時間:2022-09-15
記得很小的時候,特別喜歡用手把臉盆里的水攪成一個漩渦,然后看著漩渦的速度慢慢降下來,直到整個臉盤里的水趨于平靜。彼時,只會玩泥巴的小編只能看著這種有趣的現象一邊傻笑,一邊因為不小心把水灑在地上而被媽媽揍屁股。直到多年以后,在《流體力學》的課本上結識了粘性,小編開始理解生活中許多習以為常的流動現象,也認識到原來粘性如此重要…
01 粘性的表象
“粘”,是古漢語規范字“黏”的通俗字形式,意為橡膠或糨糊一樣的性質。而英文中viscosity一詞,則是來源于一種植物的拉丁文名稱“viscum”,也就是槲寄生,其漿果具有黏稠的特性。

槲寄生 VISCUM▲

在流體力學術語中,粘性指的是流體抗拒變形的能力。粘性越大,其抗拒外界剪切力作用的能力越強,比如攪動杯子里的水輕而易舉,但攪動糨糊或者糖漿則有些費力。

對剪應力毫無抵抗的流體被稱為理想流體或者無粘流體。不過,只有在極低溫度下的超流體才會呈現無粘的屬性,而我們常見的液體或者氣體都是有一定粘度的。具有極高粘度的流體則在一定程度接近固體屬性,比如常溫下的瀝青。
02 粘性的機理
我們都有這樣的生活經驗,粘稠的液體加熱后,通常粘度會降低。比如公園里做“轉轉糖”的老大爺,通常要把糖漿加熱到一定的溫度,才能流暢的做出各種造型。再比如在寒冷的冬季,車輛在啟動的一段時間內感覺到動力有一定的下降,換擋也不如平日那么順滑,也主要是由于發動機、變速箱等動力部件內的潤滑油粘度增加而引起。

大部分液體的粘性都會隨溫度上升而降低,但氣體卻恰恰相反——通常而言,氣體的粘度隨溫度升高而增大。而液體和氣體之所以有如此大的差異,是因為它們產生粘性的機理不同。
下圖對比了固體、液體和氣體的分子排列示意圖,可以看出來,固體分子排列緊密且有序,分子之間被分子力牢牢控制而難以發生隨意的運動。液體分子則不會保持固定的形狀,但它們仍然致密排列,就像游樂場里的海洋球,因此,液體的分子之間仍具有一定的分子力,而這也是液體粘性的主要來源。
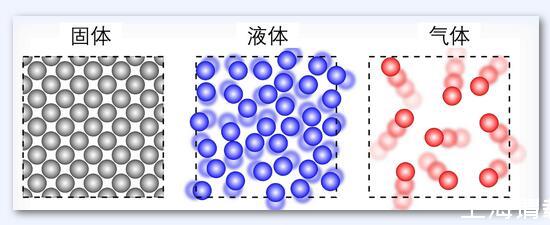
液體分子由于分子力的存在而產生了相互的“糾纏”。而所有的分子或者原子都在自身附近做無規則的振動,當液體溫度升高時,這種振動加強導致分子之間的“糾纏”變得松松垮垮,因而液體的粘度降低。事實上,局部振動也會引起液體粘度降低,比如陷入泥潭的動物越掙扎下沉的越快。
而氣體分子排列稀疏,分子之間相去甚遠,分子力不再是動量傳輸的主導,而分子間的相互碰撞則成為粘性的來源——比如上層分子運動的同時,也源源不斷到下層串門,把鄰居家也攪得雞飛狗跳,帶來動量的交換。而氣體溫度升高時,這種“串門”就更加頻繁和劇烈,下層也愈發雞犬不寧,粘度自然增大。
當然,液體內部也會存在類似于氣體一樣由于“串門”產生的動量交換,不過相比于液體的分子力而言還很小,不足以主導粘性變化。
03 粘性的科學表達
正如前面所說,人們很早便感受到了流體具有“粘”的屬性,但是如何從科學上表達流體的粘性成為了一個新的問題。作為世界物理學界金字塔尖的男人,牛頓幾乎霸屏了整個中學物理課本,當然也沒有放過流體。1686年,牛頓經過大量的實驗研究,提出了著名的“內摩擦定律”——流體的內摩擦力(即粘性力)的大小與流體的性質(粘性系數μ)有關,并與流體的速度梯度和接觸面積成正比。
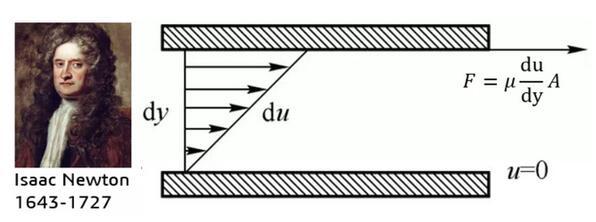
自牛頓之后,粘性系數成為描述流體屬性的一個重要參數,人們可以直觀的感受到,粘性大的流體不容易流動,而粘性小的流體很容易動起來,但是如何用流體力學的語言來描述粘性與流動的關系成為了一個問題。
距離“牛頓內摩擦定律”大約兩百年之后,還在原來的地方,另一位著名的英國物理學家雷諾通過經典的流體染色實驗揭示了流動與粘性的關系:相同的速度、密度和流動尺度條件下,粘度更低的流體更容易趨向于某種混亂的、彎曲的流動,也就是我們后來熟知的湍流。又過了20多年,著名的物理學家索末菲在第四屆國際數學大會上第一次明確以“雷諾數”命名了流體力學中最重要的無量綱數,而粘性系數便是雷諾數中不可替代的分母。

04 粘性與湍流
隨著雷諾實驗和雷諾數被提出來以后,近代流體力學,尤其是湍流理論的發展出現了一個前所未有的盛況,而粘性與湍流的關系也順理成章的轉化成了雷諾數和湍流的關系。1974年刊登于《流體力學》期刊中的一篇經典文章,通過流動顯示技術生動形象的描繪了雷諾數和流態的關系:隨著雷諾數的增大,渦旋的整體形狀和尺度基本一致,然而射流摻混的渦系結構卻越來越豐富。
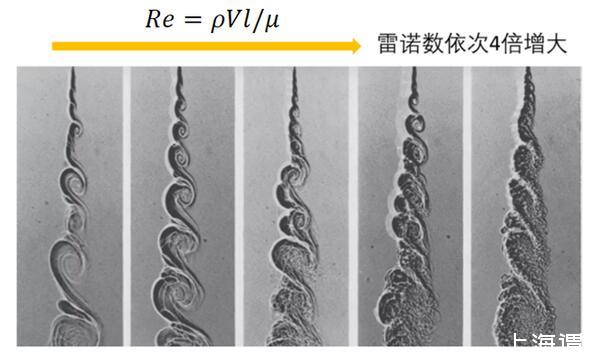
而之所以會出現上圖中的有趣現象,則要牽扯到湍流的生成、傳遞及耗散:湍流中的大渦會破碎為小渦,小渦再破碎為更小的“迷你渦”,然后逐漸耗散,這個過程與當地雷諾數相關。當“迷你渦”變得足夠小時,根據角動量守恒,渦的角速度將會非常大,意味著局部速度剪切很強,粘性就變得舉足輕重了,于是,“迷你渦”就這樣被粘性耗散掉了。事實上,渦的尺度足夠小時,體現為當地雷諾數非常小,粘性力對流體的影響則顯著大于慣性力。
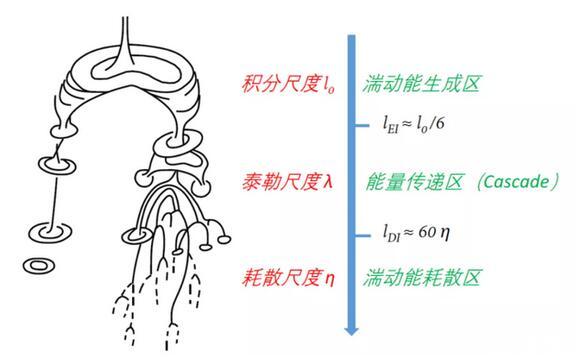
在給定特征長度(大渦尺度)和特征速度(湍流脈動速度)的條件下,流體的粘性幾乎決定了耗散渦的大小,即湍動能在什么樣的尺度上耗散。大渦的形態取決于幾何尺度,當雷諾數足夠高且幾何尺度不變的情況下,增大雷諾數并不會改變大渦的形態,但是小渦的尺度取決于湍流雷諾數,雷諾數越高的流動需要越小的渦尺度才能完成耗散,因此雷諾數越高的流動,其大渦到小渦的覆蓋尺度越復雜。
05粘性與流體力學
雖然早在1686年,牛頓就通過實驗測得了流體的粘性,可是,當我們攜帶著粘性回歸到流體力學的時候,還是會發現由于粘性的存在,使得實際流體運動的研究變得非常復雜。為了便于理論分析和公式的推導,物理學家們在流體力學中引進了“理想流體”的概念。
理想流體當然是假想的,不過研究無粘流體的運動,可以使問題大大簡化,容易得到流體流動的基本規律。1755年,數學家歐拉將微分方程應用到了流體力學的領域,并提出了影響后世的歐拉方程,即牛頓第二定律施加到理想流體上的微分方程。
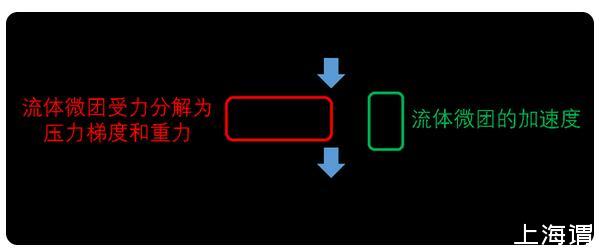
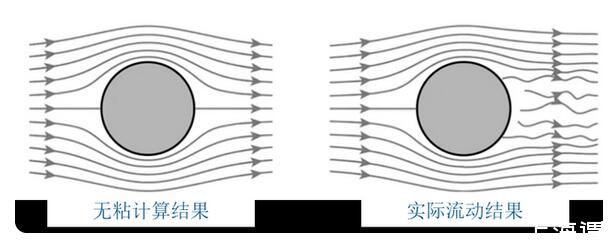
歐拉提出歐拉方程后不久,人們就認識到方程中缺乏粘性項,這會導致歐拉方程的計算結果和實際產生偏差,比如大家熟知的達朗貝爾佯謬。下圖顯示了理想流體和實際流體下圓柱繞流的對比,可以看出,無粘流動的結果和實際存在很大的差異。因此,如何在流動方程中添加粘性項成為了跨越百年的流體力學難題。
后來的我們都知道了《流體力學的“白月光”》的故事,直到1845年,結合納維對粘度的思考和柯西的張量思維,斯托克斯爵士便大展神威,推出了引無數流體人盡折腰的“N-S方程”,該方程定義為“描述粘性不可壓縮流體動量守恒的運動方程”。迄今為止,該方程仍然是流體力學領域里最通用的流體運動方程。

值得一提的是,對某些粘性影響不大的流動問題,忽略粘性所得到的結果與實際結果往往差別不大。而對于高雷諾數的湍流,在主流中使用歐拉方程,而在粘性影響較大的邊界層中使用邊界層方程或者經驗公式,也能得到不錯的結果。
06物理粘性之外的粘性
粘性是流體流動的穩定器所言非虛。而CFDer都知道,對于數值計算而言,粘性也至關重要。不過在傳統CFD算法中,除了物理粘性之外,還有湍流粘性和數值粘性兩個妖魔鬼怪。湍流粘性
湍流粘性來源于雷諾平均的N-S方程,下式中多出來的脈動應力項,稱之為雷諾應力。1877年Boussinesq借助于牛頓切應力公式,提出了影響深遠的渦粘性假設:雷諾應力正比于時均速度梯度,其中比例系數μt表征了湍流脈動引起的切應力效應,稱為渦粘性系數。
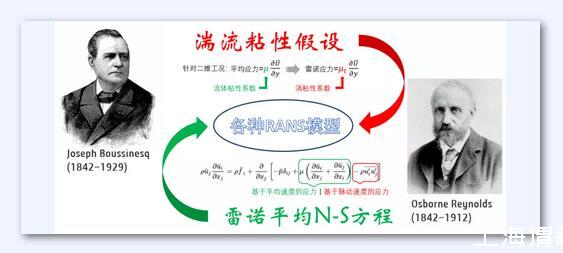
湍流粘性雖然是人為定義的,但是也具有相對清晰的物理含義:由于湍流的“上躥下跳”,給不同速度的流體帶來更多的動量交換,類似于物理粘性對流動帶來的影響。當然,湍流粘性的更大意義在于,CFDer們逃脫了直接求解NS方程的魔咒,轉而走向CFD的工程實用化。數值粘性
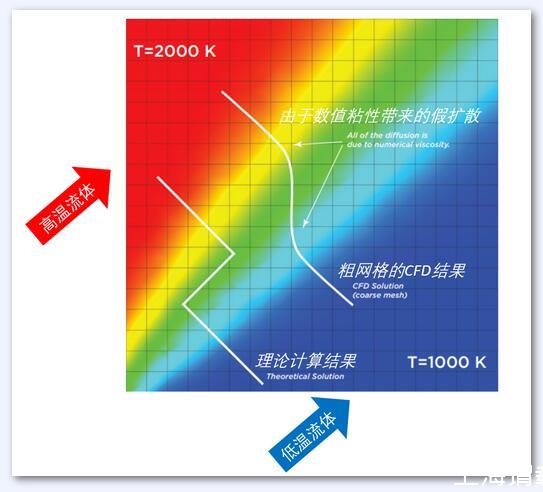
而數值粘性則完全是從微分方程離散到差分方程的過程中產生的誤差。從數學推導而言,相比于原始的微分方程,從差分方程導出的修正方程中有多余的項。其中二階項的系數對應常規N-S方程中二階項的系數,類似于方程中的物理粘性,因此被稱為數值粘性。
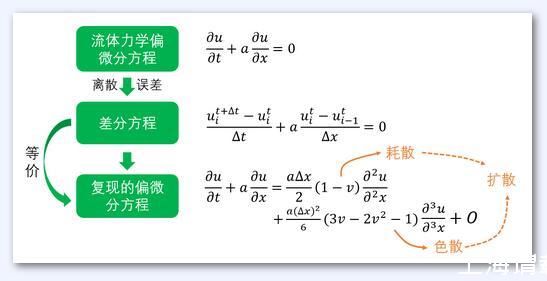
數值粘性實際上是來源于空間離散的步長是一個有限的小量(而不是無限小),這引起了物理變量在這個小范圍內的平均,其效應相當于擴散,并帶來了額外的動能耗散,也即是粘性。
不同于湍流粘性有相應的物理含義,數值粘性則由對方程的離散處理而來。增加數值粘性對流場的影響,本質上和增大物理粘性類似,比如使分離區減弱、激波變寬抹平等,本質上改變了整個流場的熵。而從雷諾數的角度理解,增大數值粘性意味著減小了有效雷諾數,從而改變了流態。
從網格離散的那一刻起,數值粘性便隱含在離散方程的迭代中,降低了解的精度。不過數值粘性也常常有利于收斂,堪稱CFD的穩定器。而在許多CFD的應用中,數值方法中隱含的數值粘性還不夠,求解容易發散,因此人們還會顯性添加更多的數值粘性。在《計算流體力學基礎及應用》的書中,作者建議道:對于那些必須使用人工粘性的問題,審慎的運用大概率都能獲取合理的、有時甚至相當精確的解。但重要的是,你必須知道自己在做什么。
結語
粘性作為流體的穩定器,多年以來讓CFDer們又愛又恨。而給自己的程序中添加粘性時,我們仿佛化身食堂打菜的大媽,每舀起一勺總要忍不住抖三抖,生怕加的多了。不過望著窗外可憐的快要發散的小眼神,又忍不住糾結起來。










