合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
推薦新聞Info
-
> 定性分析聚合物界面張力與系統黏度比之間的關系——數值仿真結果、結論
> 定性分析聚合物界面張力與系統黏度比之間的關系——數值模擬、實驗研究結果
> 定性分析聚合物界面張力與系統黏度比之間的關系——實驗部分
> 探究LB復合膜的酸致變色特性
> 受磷脂雙分子層啟發構建ZIBs兩性LB膜——制備高性能碘正極新思路
> 納米活性顆粒表面潤濕性測量方法及具體操作步驟
> 人工沖洗升級為超聲波清洗,可改善新能源電池沖壓配件的表面張力
> LB法組裝Silicalite-1型分子篩晶粒層,制備出高度b-軸取向的ZSM-5分子篩膜
> 微量天平高靈敏測定雞肉中磺胺類藥物含量
> 超低軌衛星環境效應研究也會用到超微量天平?
不同成分、溫度條件下鋼液的表面張力計算方法
來源:東北大學 瀏覽 156 次 發布時間:2024-06-12
表面張力是鋼液的重要物理性質之一,對于鋼材潔凈度控制及凝固成型過程均具有重要影響。鋼液表面層和內部粒子所處的環境不同,兩者所受的力并不相同,使鋼液表面產生自發縮小傾向的力稱為鋼液的表面張力。鋼液的表面張力不僅對新相的生成有影響,而且對相間反應、渣鋼分離、鋼液對耐火材料的侵蝕等也產生影響,準確獲取鋼液的表面張力對于優化冶煉過程、改善鋼材質量、提升生產效率具有重要意義。
目前,表面張力主要通過實驗測定方法獲得,對于液態金屬,常用的是氣泡最大壓力法和靜滴法。影響鋼液表面張力的因素眾多,主要包括鋼液成分、溫度及鋼液的接觸環境,對于鋼液來說,溫度通常在1700K以上,一方面,高溫條件的穩定獲得難度較高,即溫度精確控制難度較高,對表面張力的測定精度存在影響,另一方面,高溫鋼液極易與接觸介質發生反應,即鋼液成分難以穩定控制,測得的表面張力易于偏離真實值;再者,真實鋼液組元復雜,各組元對表面張力的交互影響難以充分分離;另外,鋼液表面張力高溫測定還存在流程復雜、成本高等不足。
近年來,隨著計算機硬件及計算機數值模擬技術快速發展,其中分子動力學(MD)是一種利用牛頓運動定律模擬原子或分子系統的強大方法,可從微觀尺度解析物理化學過程,目前已成為研究材料微觀結構和性能的有效方法,在高溫冶金熔體領域應用也逐漸擴展。
鑒于現有表面張力獲取技術存在的不足,東北大學閔義團隊供一種采用模擬計算獲取鋼液面張力的方法,即采用分子動力學模擬的方法計算鋼液原子尺度的微觀結構信息,并以此為基礎獲取不同成分、溫度條件下鋼液的表面張力,該方法可有效避免傳統高溫實驗測定方法的數據波動大、影響因素難以分離及成本高等問題;另外,本方法基于鋼液的微觀結構信息獲得表面張力,可深化對表面張力產生本質的理解及影響因素的解析,對于鋼液表面張力控制可提供明確指導。
Fe-C二元體系-真空基于微觀結構解析的鋼液表面張力計算方法:
(1)根據冶金鋼液的主要化學成分,鋼液由Fe-C二元體系組成,具體成分為Fe:99.85%,C:0.15%。
(2)Fe-C二元體系的原子數設定為12000個,根據Fe-C二元體系中各組分的摩爾比,可確定不同原子的個數,之后再根據Fe-C二元體系在高溫液態條件下的密度,可計算出模擬盒子的邊長,具體如表1所示。

表1Fe-C二元體系的原子數、密度和盒子邊長

基于表2中的原子種類、個數及Fe-C二元體系的密度,采用Materials Studio軟件建立Fe-C二元體系的初始結構模型,得到一個包含原子數目、原子類型數目、各類型原子質量、原子ID及該原子ID所對應的原子類型和x、y、z三個方向的坐標值的初始結構data文件。
(3)選取改進嵌入原子法(MEAM)作為描述Fe-C二元體系中所有原子間相互作用力的勢函數。
(4)設置模擬計算的參數,編寫執行LAMMPS軟件分子動力學模擬計算所需的in文件,將建立的Fe-C二元體系初始結構模型信息導入LAMMPS軟件進行分子動力學模擬計算。原子類型設置為atomic,采用周期性邊界條件,整個模擬過程使用正則系綜(NVT),模擬過程中原子數、體積和溫度不變,采用Parrinello-Rahman法和Nose-Hoover熱浴法進行壓力和溫度的控制。根據高斯速度分布給出了鐵原子的初始速度分布。體系的牛頓運動方程的數值解法采用Verlet算法進行求解,步長設置為1fs,每1000步保存一次數據,一共運行510000步。首先在初始溫度為4273K下運行60000步,采用共軛梯度法使初始結構的能量最小化,使體系充分混合及能量穩定。接下來,通過100000個時間步長使體系降溫到1950K,并在1950K下繼續弛豫50000步。沿z軸方向在盒子的兩側加入兩個真空區,形成平行于z軸方向的真空-液體-真空夾層結構,對擴大后的系統在1950K下弛豫300000步,為了防止液膜的游走,在每個MD步驟中都要調整系統的質心位于系統的中心,并在此階段收集計算微觀結構信息和表面張力所需的數據,最后得到模擬體系的原子坐標文件、壓力張量等模擬結果數據。
(5)將得到的原子坐標文件導入OVITO、VESTA和VMD軟件中進行可視化分析并計算模擬體系的微觀結構信息,得到模擬體系的微觀結構圖;計算表面張力所需數據收集前后模擬體系的微觀結構,將各個類型的原子進行區分,計算出不同原子對之間的徑向分布函數;根據計算得到的徑向分布函數第一峰橫坐標值得出不同原子對之間的鍵長(最近鄰距離),將徑向函數的第一峰進行積分可得出不同原子對之間的配位數。可導出模擬盒子不同區域的原子坐標文件用于微觀結構信息計算。
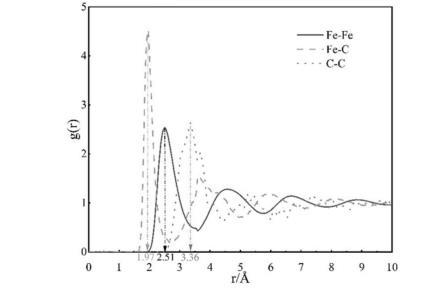
Fe-C二元體系經計算得到的徑向分布函數,Fe-Fe、Fe-C、C-C原子對的平均鍵長分別為若原子間距離小于相應的鍵長值則表示兩個原子之間互相連接,根據碳原子連接的鐵原子個數,可將鐵原子區分為自由態鐵原子(與碳原子沒有配位關系)、A型鐵(只與1個碳原子形成配位關系)、B型鐵(與2個或更多的碳原子形成配位關系)三種類別,根據模擬結果數據可對鐵原子的配位方式進行分析。
(6)根據收集的計算表面張力所需的數據,采用此鋼液表面張力計算方法計算Fe-C二元體系的表面張力。計算得到的法向壓力張量和和切向壓力張量之差PN-PT、表面張力σ和密度ρ沿z軸的分布,Fe-C二元體系的表面張力σ經計算為1.531N/m。
小結
根據壓力張量與表面張力的關系,提供了一種從原子尺度預測計算鋼液表面張力的方法,可獲取不同成分和溫度條件下鋼液的表面張力,可有效避免傳統高溫實驗測定影響因素難以分離、流程復雜及成本高等問題,可用于填補實驗數據的空白;結合鋼液的微觀結構信息,可對鋼液表面張力進行微觀結構解析,從而為鋼液表面張力的控制提供理論指導。










