合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
極復雜問題背后的簡潔數學
來源:ZAKER 瀏覽 431 次 發布時間:2022-09-21
想象一下,如果有一個微微彎曲的軟質曲面,類似一片隱形眼鏡,而我們想把它壓平,它的表面就會出現一些"多出來"的材料,進而產生褶皺。但是,這些褶皺會在什么地方出現?它們又會以怎樣的方式排列?這些我們都不清楚。
褶皺背后的科學原理通常被認為非常復雜,同時,當物體出現褶皺后,它的一些性質往往也會改變,如果想用模型模擬它們,情況也在不斷變化。
但近期,一項新研究利用實驗、模擬外加數學證明發現,通過一些簡單的幾何學,就有機會預測這些褶皺的模式,包括它們將在哪里形成,以及在某些情況下它們的方向。論文已于近期發表在《自然·物理學》上。
探索幾何原理
對一個曲面來說,曲率可以簡單理解成衡量它"有多彎"的標準。曲率可以是正的,比如圓球形狀的棒球或地球儀,它也可以是負的,比如馬鞍的形狀。還有一些是平面材料,就像我們熟悉的一張紙。
在這項研究中,團隊把重點放在具有正曲率和負曲率的彎曲外殼,重點分析材料的物理形狀和曲率對褶皺的模式可能產生多大的影響。
他們在一個像球體或馬鞍形狀的弧形玻璃表面上放置一塊平坦的塑料片,然后旋轉它,使塑料片變薄并塑形。然后,他們把塑料片放在水面上,水的張力可以提供一種穩定的壓扁的力,使表面形成褶皺。
對于每種形狀,研究人員會根據研究出的基本原理來解決理論問題,然后得出預測結果。基于這些發現,他們隨后又進行了模擬,將各個形狀和相關參數輸入一個計算機程序。
通過大量模擬和實驗,以及不斷完善過程并擴展原始理論,團隊逐步發現,通過應用一些直接的幾何原理,他們就可以提前預測出褶皺的模式,以及一個被稱為"有序"褶皺的子集的皺紋走向。
青色實線表示預測的褶皺模式。沒有這些線的區域是無序的。對于馬鞍形(曲率κ<0)的情況,褶皺向白色軸線方向衰減。對于球形(κ>0)的情況,褶皺向邊界衰減。青色虛線代表預測中使用的理想形狀。(圖/Tobasco,I.et al.,2022)
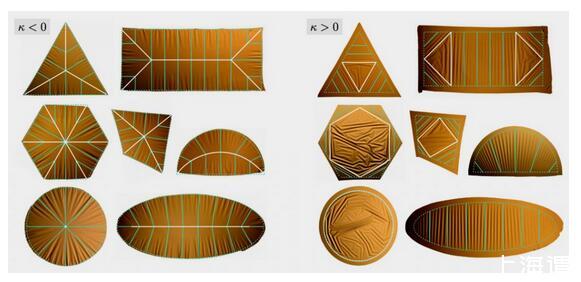
比如,對于像上圖這樣相對簡單的形狀,當曲率為正的時,形狀外部部分將包含有序褶皺,這些褶皺有組織、有秩序地發展。同時,在新劃分出的內部多邊形里(白色實線范圍內),褶皺仍舊會形成,但它們是無序且不可預測的。
簡潔而美麗的規則
研究人員認為,這項成果的最大魅力之一在于,它非常簡潔。褶皺背后的理論相當復雜,在實驗和模擬中觀察到的許多模式都不簡單。但事實證明,在一定的條件下,仍可以用一套相對簡潔的規則來預測褶皺的布局。
這很有啟發性。它也意味著,現在科學家有了一種快速、有效的方法來設計這類褶皺的模式。特別是對于那些具有允許粘附或流體流動等功能的褶皺表面。比方說,空氣中存在水分。水在山谷和山丘不平的表面上會產生不同行為。通過控制褶皺模式,也許就可以影響水的凝結方式。
研究人員希望繼續深入了解這些復雜的紋理表面,比如,如何從那些無序的褶皺中提取模式,為什么有序和無序的域可以共存,等等。
但無論如何,發現一個復雜問題的簡潔且優美的解決方案,這本身就非常令人興奮。










