合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
表面張力自由能的分子論含義
來源:知乎 阿黃sweetgirl 瀏覽 781 次 發布時間:2021-07-17
毛細作用的尺度在微米到毫米之間,其所處的尺度是連接宏觀與微觀的橋梁。表面張力不但與表面化學性質(分子層次)有關,還與宏觀的現象,比如毛細浸潤,毛細上升等現象有關。從分子層次上去理解表面能,表面張力的概念,對界面的微觀認識具有重要的意義。
下面我們從分子論的角度來認識表面自由能。
表面自由能定義為“將本體沿某一界面分開克服本體內分子間內聚引力的作用所需要做的可逆功”。這種克服內聚引力所做的功以勢能的形式儲存在新產生的表面上,就是表面自由能。
按照分子理論,兩個分子間存在Van der Waals力,對應存在兩分子間的van der Waals相互作用勢,其表達式為
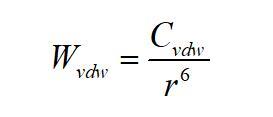
式中,Cvdw為Van der Waals分子對作用勢系數,且
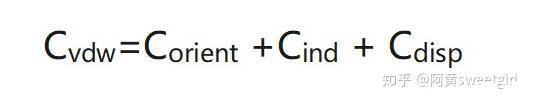
其中,Corient為Kessom分子對取向作用勢系數,Cind為Debye分子對誘導作用勢系數,Cdisp為London分子對色散作用勢系數。為分子方便,把原公式中負號去掉,即把吸引作用是為正。
而兩分子間的Van der Waals力的大小和表示為:
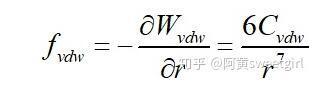
其方向沿兩分子的連線方向。
對于物體系統來說,按照Hamaker理論,物體系統的總作用勢等于各個分子間互相作用勢的疊加,即
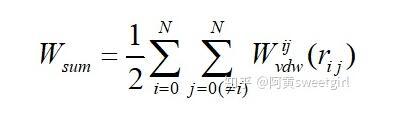
式中Wij是分子i和分子j間的不受其他分子影響的互作用勢;rij是分子i和分子j間的距離;N為總分子數。
根據這一原理,單個分子與有限厚無限大平板的互作用勢為
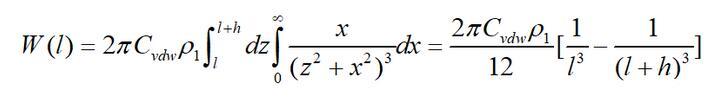
始終ρ1為無限大平板物體單位體積的分子數(分子密度);h為平板的厚度;l為單個分子到平板的最近距離。
當厚度取無限大時可得單個分子與半無限體間的互作用勢為
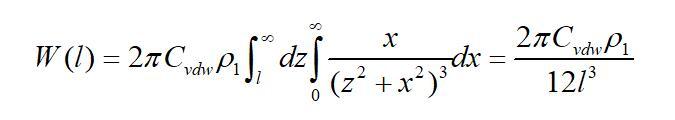
將單個分子換成有限厚無限大平板的單位面積,可得有限厚無限大平板之間的互作用勢為
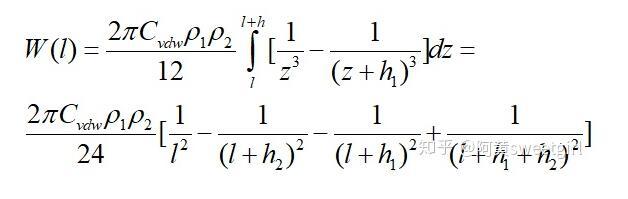
式子中h1和h2分別為兩無限大平板的厚度。
當h1趨近于無窮時,得有限厚無限大平板與半無限體的互作用勢為
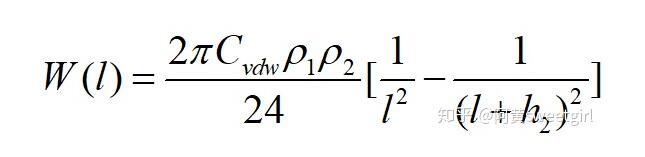
當h1和h2都趨近于無窮時,得兩半無限體之間的互作用勢為
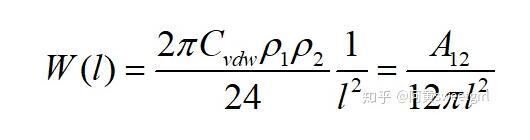
式中A12為Hamaker常數。定義為:
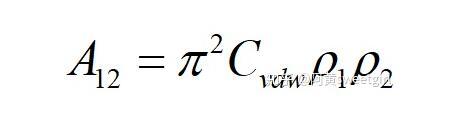
若取l為物質本體內分子間的距離d11,且兩半無限體為同一種物質時,則上式的互作用勢變為(取絕對值
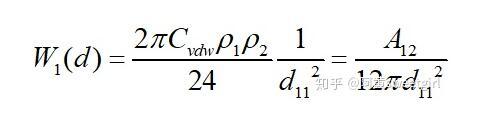
式中,
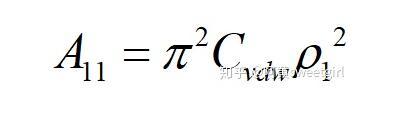
為物質1的Hamaker常數。該作用勢能就相當于本體的內聚功。從表面自由能的定義不難看出,當將本體沿本體內的一個界面分開時,單位面積需要克服內聚力所做的功就等于這個作用勢能。由于分開后形成兩個新表面,因此每個表面上的勢能等于該勢能的一半。因此物體的表面自由能(表面張力)也等于該作用勢能的一半,即
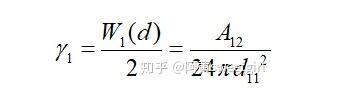
同樣,若取l為兩相界面處分子間的距離d12,且兩半無限體為兩種不同的物質時,則互作用勢變為
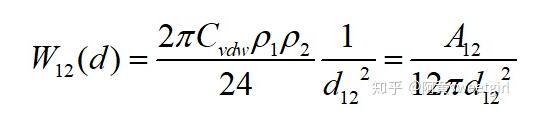
該作用勢能就相當于兩相之間的粘附功。由于粘附功與表面張力(自由能)和界面張力(自由能)有如下關系:
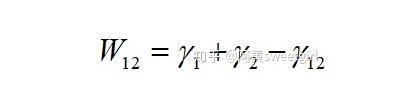
式中γ12為界面張力(自由能)。則界面張力/自由能可表示為:
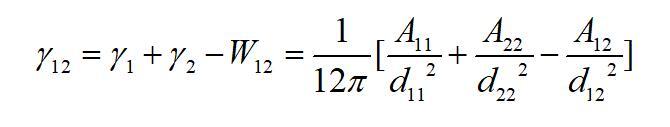
式中d11為物質1的分子間距;d22為物質2的分子間距;d12為物質1和物質2在界面處的分子間距;A11、A22及A12分別為物質1本體內、物質2本體內及物質1與物質2之間的Hamaker常數。
參考:節選自《毛細力學》第三章,高世橋,劉海鵬,科學出版社,2010.










